Today in this article we will discuss about the types of number systems. The description of each number system will be given here.
Anything that refers to the measurement of things is known as number. The system of counting or expressing a number is called number system.
That means number system is the method of expressing or writing a number and performing various calculations like addition, subtraction, multiplication, division etc with these numbers.
The fundamental symbols to write any number of a system is called digit. So, digit is the smallest symbol to make a number. For example, 123 is a number which consists of 3 digits 1, 2 and 3.
In this guide, we will discuss broadly about different types of number systems and after that I will try to explain the conversion of number from one system to another. Now, let’s be familiar with different types of number systems.
Table of Contents
ToggleTypes of Number Systems
Every number system that invented still now are categorized in two vast types of number systems.
Then the last one is sub divided into many categories from which I will discuss about most uses 4 types of number systems here. See the list bellow;
- Non-positional number system
- Positional number system
- Binary Number System
- Octal Number System
- Decimal Number System
- Hexadecimal Number System
1. Non-positional number system
Non-positional number system is the oldest method of counting a number. The digits have no their positional value in this number system.
The total value of a number is determined by individual value of every digit. It is very complex to perform mathematical calculation in this number system.
For this, there is no available use of this number system today although in ancient times it has been used.

Roman number system is the existing example of non-positional number system. In roman number system value of x is 10 and for this xxx is equivalent to 30. Here, x has no positional value.
2. Positional number system
Now a days we are using positional number system to perform our daily mathematical calculations.
In this types of number systems every digit has a positional value and this positional value depends on the method of writing this number.
To know the actual value of a number in positional number system we have to know the value of every digit, base of the writing method and position of every digit.
For example, in decimal number we use 10 digits from 0 to 9 and the positional value depends on the position of these digits.
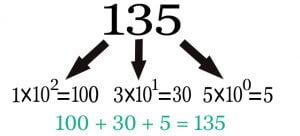
In positional number system every number is divided into two part of integer and fraction by a radix (.) point.
Suppose a decimal number 135.265
Here, 135 is the integer portion, (.) is the radix point and 265 is the fraction part.
Types of positional number system
There are mainly 4 types of positional number system we use still today. Other types have no practically used now a days.
So, we should learn only this 4 types. You will get the idea of other types of number by learning these systems.
- Binary Number System
- Octal Number System
- Decimal Number System
- Hexadecimal Number System
Binary number system
There are only two digits to write a number in binary number system. These are 0 and 1. For this, the base of binary number system is 2.
So, the number system in which only two digits are used to write any number is called binary number system.
The shape of a number is largest compare to other number system as there are only two digits to express a number in binary number system.
Every electronic device including computer use this number system to perform mathematical calculation. Every digit is called bit (binary digit) in binary number system.
For example, (1011001)2 is a binary number which consists of 7 bits. We can easily convert a binary number to octal, decimal or hexadecimal number which we will discuss later.
Octal number system
Meaning of octal is eight. In octal number system total eight digits can use to express a number and they are 0, 1, 2, 3, 4, 5, 6 and 7.
For this, the base of octal number system is 8. So, the number system in which total 8 digits are used to write any number is called octal number system.

It needs minimum two digits to write a number greater than 7 in octal number system. Consider, (127)8 is an octal number which consists of 3 digits 1, 2 and 7.
Decimal number system
Decimal number system is the most popular number system which we use in our normal life. In decimal number system we use 10 digits to write any number which are 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9.
For this, the base of decimal number system is 10. So, the number system in which we use total 10 digits to express any number is called decimal number system.

For example, (99)10 is a decimal number which consists of 2 digits 9 and 9. We can easily convert a decimal number to equivalent binary, octal or hexadecimal number.
Hexadecimal number system
In hexadecimal number system we can use total 16 digits to write a number. These are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A (10), B (11), C (12), D (13), E (14) and F (15).
For this, the base of hexadecimal number system is 16. So, the number system in which total 16 digits can be used to write any number is called hexadecimal number system.

For example, (7D)16 is a hexadecimal number which consists of 2 digits 7 and D. Learn how to convert a hexadecimal number to its equivalent binary, octal or decimal number.
Comparison among binary, octal, decimal and hex
Here is a simple comparison among four main number systems. You can get a clear concept about all the main number systems seeing this table bellow;
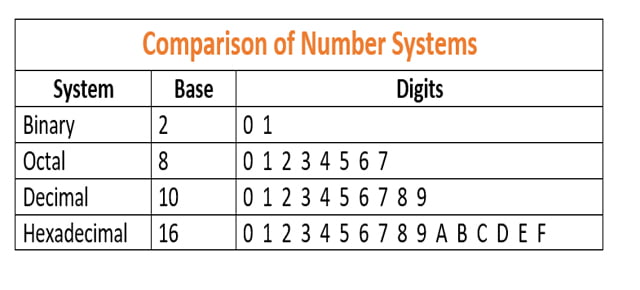
Now, think about some different types which may 4 based, 5 based or 6, 7 9 etc. All you have to think that there will be the same number of digits as their base. You will learn details in our next several posts.
I hope, now you have no doubt about different types of number systems which we have discussed here in this post. This can be a very useful post for you we believe.
Please tell us your experience and opinion about this post at the comment section bellow. Was this post helpful or not. We will be very happy to hear from you.





Good article. I’m facing many of these issues as well..
I am actually grateful to the owner of this web
site who has shared this fantastic article
Hello my friend!
I wish to say that this article is awesome, nice written and come with approximately
all vital infos.
I’d like to look extra
posts like this .
Great article. I am experiencing a few of these issues as well..
You completed some good points there. I did a search on the subject and found a good number of folks will consent with your blog.
These are in fact great ideas in about blogging.
You have touched some pleasant points here. Any way keep up wrinting.