Here, we you will learn binary to hexadecimal conversion of number system with related examples.
In binary number system we can only use 0 and 1 to write any number. But for hexadecimal number system we can use total 16 digits to write a number where we use the digits 0 to 9 and character A to F.
In this article we will learn to convert a number from binary to hexadecimal. We can convert a number using two rules where the first rule is for integer and second rule is for fraction part of that number.
Table of Contents
ToggleBinary to hexadecimal conversion
Binary to hexadecimal: integer part
- Take every 4 bit from right to left and fill up by taking zeros if there is not available digit at the left to consist 4 bits.
- Replace every 4 bit by their equivalent hexadecimal value.
Example : Convert 101111001112 to equivalent hexadecimal number
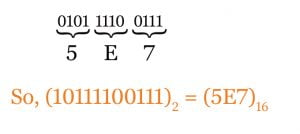
As like as our generally used decimal number, here also we can take necessary zeros at the right side of decimal point and left side before decimal point to convert from binary to hexadecimal.
This rule works as our generally used decimal number that we can write 71 instead of 071 and 223 instead of 0223.
Binary to hexadecimal: fraction part
- Take every 4 bit from left to right and fill up by taking zeros if there is not available digit at the right to consist 4 bits.
- Replace every 4 bit by their equivalent hexadecimal value.
Example : Conversion of 0.110011010012 to equivalent hexadecimal number.

We can take necessary zeros at right as well as ignore unnecessary zeros from right, when we convert the fraction part of binary to hexadecimal. We can write 0.111 instead of 0.1110 and 101 instead of 0101
See the bellow example where we have converted a full binary number to its equivalent hexadecimal number. This may help you to understand the topics.
Example : Conversion of 10100110.101012 to equivalent hexadecimal number
To convert this number from binary to hexadecimal we can convert whole number by a single rule which will apply at both it’s integer part and fraction part.
We should ignore zeros at left side of integer and right side of fraction part and take necessary zeros at left side of the integer and right side of the fraction part.
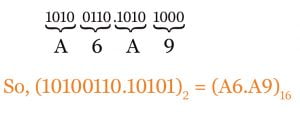
So, total hexadecimal equivalent of this binary number will be (A6.A9)16. You can convert any binary number to its equivalent hexadecimal number by this rule.
Please tell us in the comment section if you have any doubt still now.



I’ve been exploring for a little for any high-quality articles or weblog
posts in this kind of space . Exploring in Yahoo I finally stumbled upon this web site.
Reading this info So i’m satisfied to convey that I’ve an incredibly excellent
uncanny feeling I discovered exactly what I needed.
I most undoubtedly will make sure to do not
fail to remember this website and give it a glance
regularly.
I used to be able to find good info from your content.
Usually I don’t read post on blogs, but I wish to say that this write-up very compelled me to try and
do so! Your writing taste has been amazed me. Thanks, very great article.
That is a great tip especially to those fresh to the blogosphere.
Short but very precise information… Thanks for sharing this one.
A must read post!
It’s going to be finish of mine day, however before ending
I am reading this enormous paragraph to improve
my know-how.
My brother recommended I might like this blog.
He was entirely right. This post actually made my day.
You cann’t imagine just how much time I had spent for this information! Thanks!