Before learning hexadecimal to binary number conversion, we should learn about this two number systems.
The most uses 4 number systems are binary, octal, decimal and hexadecimal number systems.
Binary number system is two based number system where only two bits are being used. These are either 0 or 1. This is a very important number system for computer hardware systems.
All the components inside a computer can only understand this number system. So, we must have to learn about this binary number system.
You can learn more about main 4 number systems which we already have published.
However, the hexadecimal number system is a 16 based number system and we can use the digits 0 to 9 with the alphabet A, B, C, D, E and F for constructing any number. This is also a very useful number system for computer system.
We will learn to convert a number from hexadecimal to binary in this number conversion guide. We will use separate rules for fraction and integer part of the hexadecimal number to convert it to the equivalent binary number.
So, let’s get started without extending more. We will see the general rules for converting a number form hexadecimal to binary first.
Table of Contents
ToggleHexadecimal to Binary Conversion
Hexadecimal to Binary: integer portion
- Replace every hexadecimal digit by their equivalent binary value of 4 bits.
- Write them one after another with the same order as hexadecimal number.
These rules might be a little bit difficult for you to understand. But if you see the following example where we have converted a number from hexadecimal to binary, then it will be clear to you.
Example: Conversion of (2B8)16 to equivalent binary number
This is an integer hexadecimal number and we have to convert it from hexadecimal to binary integer number. The main conversion is as like as the figure we have given bellow.
We will write the equivalent 4 bits of each hexadecimal digit. Then the equivalent binary number will be gotten. Here we have just applied this rules.
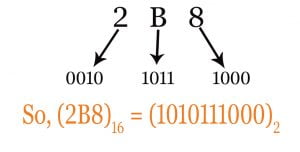
At the time of converting we can ignore zero at left. That means 01101 and 1101 has the same meaning. At the same time, we can also take necessary zeros at the left side for integer number.
You can now convert any integer hexadecimal number to equivalent binary number by these rules and I hope you will be able to do that now.
After this conversion for integer number from hexadecimal to binary we will now learn to convert a fraction number from hexadecimal to binary with necessary examples.
Similarly as like as integer, here also we will use some rules for converting the number. The rules are given bellow here.
Hexadecimal to Binary: fraction portion
- Replace every hexadecimal digit by their equivalent binary value of 4 bits.
- Write them one after another with the same order as hexadecimal number.
All these rules are the same as integer conversion. Here we will use the same method for converting the given number from hexadecimal to binary.
Although the rules are same, we will see an example here also to give you a clear idea about conversion of fraction part from hex to binary number. See the example bellow.
Example: Conversion of (0.28C)16 to equivalent binary number
We have to write the equivalent 4 digits binary number for each hexadecimal digits. Then we will get the whole binary equivalence number.
The concept of zeros is also same here. See the given figure of conversion.
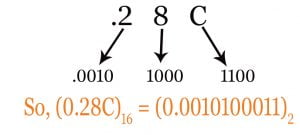
Here also we can ignore zero at right, when we convert a fraction number from hexadecimal to binary. This rule is as like as decimal number where we can write o.43 instead of 0.430
If you can understand this two conversion of hexadecimal to binary, then that’s all what you have to learn. You are now able to convert any number from hexadecimal to binary.
All you have to do is just practice some random example conversion to become more expert. I hope, you will be able to that.
I have given a complete example of such conversion which may help you to become more expert.
See the complete example given bellow to convert a number from hexadecimal to binary if you have any doubt still now. It may help you to understand the conversion.
Example: Convert (CD4.28C)16 to equivalent binary number
Here, we will convert the whole number from hexadecimal to binary using a single rule. We need not to convert the integer and fraction part separately.
However, we will ignore zero at left side of integer and right side of fraction part as like as other number systems.
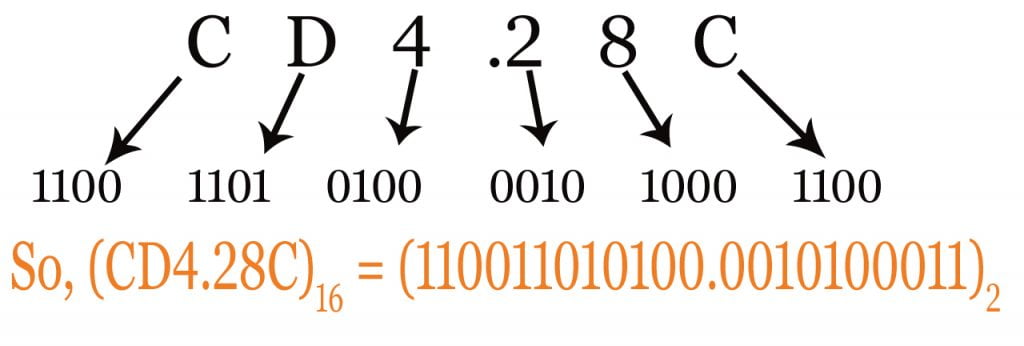
The total binary equivalent of this hexadecimal number is (110011010100.0010100011)2 . You can convert any hexadecimal number to its equivalent binary number by using the rule.
Now, it is your time to practice more. I hope this guide was very helpful to you for learning this conversion. I have made this post very easy to understand with necessary photos of conversion.
After seeing everything, if you find any unexpected mistake here, then please tell us to help other readers. We will appreciate you for this.
Please tell us your experience and opinion in the comment section bellow. This will really inspire us. Thank you for remaining with world tech journal.





This design is steller!
You obviously
know how to keep a reader entertained. Between your
wit and your videos, I was almost moved to start my
own blog (well, almost?HaHa!) Wonderful job.
I really enjoyed what you had to say, and more than that, how you
presented it. Too cool!